como bill gates cuenta la historia, Warren Buffett una vez lo retó a un juego de dados. Cada uno seleccionaría uno de los cuatro dados pertenecientes a Buffett, y luego tirarían, y ganaría el número más alto. Estos no eran dados estándar, tenían una variedad de números diferente a la habitual del 1 al 6. Buffett se ofreció a dejar que Gates eligiera primero, para que pudiera elegir el dado más fuerte. Pero después de que Gates examinó los dados, devolvió una contrapropuesta: Buffett debería elegir primero.
Gates había reconocido que los dados de Buffett exhibían una propiedad curiosa: ninguno de ellos era el más fuerte. Si Gates hubiera elegido primero, cualquiera que fuera el dado que eligiera, Buffett habría podido encontrar otro dado que pudiera vencerlo (es decir, uno con más del 50 por ciento de posibilidades de ganar).
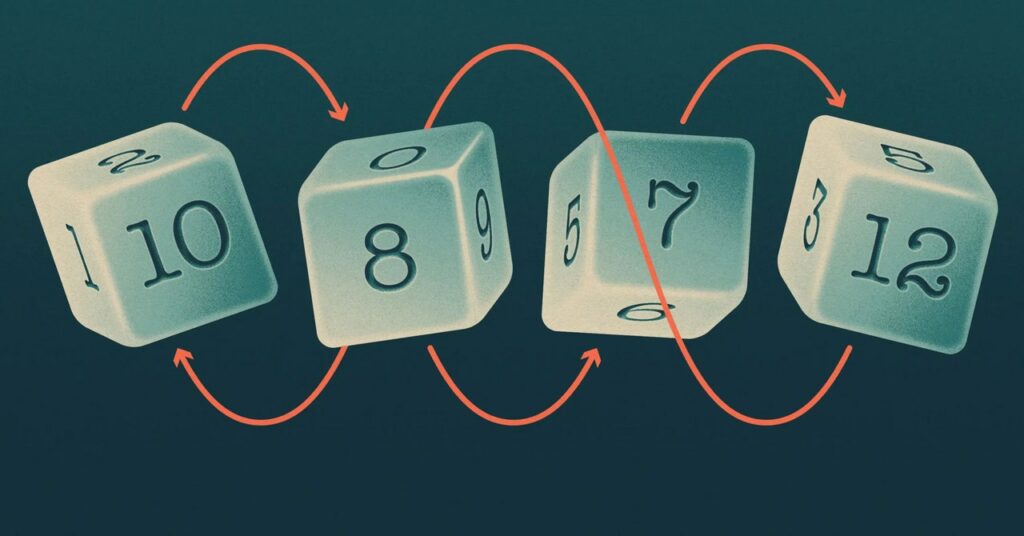
Los cuatro dados de Buffett (llámalos A, B, C y D) formó un patrón que recuerda a piedra, papel o tijera, en el que A latidos B, B latidos C, C latidos Dy D latidos A. Los matemáticos dicen que tal conjunto de dados es "intransitivo".
“No es nada intuitivo que [intransitive dice] debería existir”, dijo Brian Conrey, director del Instituto Americano de Matemáticas (AIM) en San José, quien escribió un artículo influyente sobre el tema en 2013.
Los matemáticos dieron con los primeros ejemplos de dados intransitivos hace más de 50 años, y finalmente demostraron que si consideras dados con más y más lados, es posible crear ciclos intransitivos de cualquier longitud. Lo que los matemáticos no sabían hasta hace poco era cuán comunes son los dados intransitivos. ¿Tienes que idear estos ejemplos con cuidado, o puedes elegir dados al azar y tener una buena oportunidad de encontrar un conjunto intransitivo?
Mirando tres dados, si sabes que A latidos B y B latidos Ceso parece una prueba de que A es el más fuerte; situaciones donde C latidos A debe ser raro. Y, de hecho, si se permite que los números en los dados sumen diferentes totales, entonces los matemáticos creen que esta intuición es cierta.
Pero un artículo publicado en línea a fines del año pasado muestra que en otro entorno natural, esta intuición falla espectacularmente. Suponga que necesita que sus dados usen solo los números que aparecen en un dado normal y que tengan el mismo total que un dado normal. Entonces, el papel mostró, si A latidos B y B latidos C, A y C tienen esencialmente las mismas posibilidades de prevalecer unos contra otros.

Otras noticias que te pueden interesar