En el otoño de 1972, Vance Faber era un nuevo profesor en la Universidad de Colorado. Cuando dos matemáticos influyentes, Paul Erdős y László Lovász, vinieron de visita, Faber decidió organizar una fiesta de té. Erdős en particular tenía una reputación internacional como investigador excéntrico y enérgico, y los colegas de Faber estaban ansiosos por conocerlo.
“Mientras estábamos allí, como en muchas de estas fiestas de té, Erdős se sentaba en un rincón, rodeado de sus fans”, dijo Faber. "Mantendría discusiones simultáneas, a menudo en varios idiomas, sobre diferentes cosas".
Erdős, Faber y Lovász centraron su conversación en los hipergráficos, una nueva idea prometedora en la teoría de grafos en ese momento. Después de algún debate, llegaron a una sola pregunta, más tarde conocida como la conjetura de Erdős-Faber-Lovász. Se refiere al número mínimo de colores necesarios para colorear los bordes de los hipergráficos dentro de ciertas restricciones.
“Fue lo más simple que se nos ocurrió”, dijo Faber, ahora matemático en el Centro de Ciencias de la Computación del Instituto de Análisis de Defensa. “Trabajamos un poco en eso durante la fiesta y dijimos: 'Bueno, terminaremos esto mañana'. Eso nunca sucedió."
El problema resultó ser mucho más difícil de lo esperado. Erdős lo publicitó con frecuencia como una de sus tres conjeturas favoritas, y ofreció una recompensa por la solución, que aumentó a $ 500 cuando los matemáticos se dieron cuenta de la dificultad. El problema era bien conocido en los círculos de la teoría de grafos y atrajo muchos intentos para resolverlo, ninguno de los cuales tuvo éxito.
Pero ahora, casi 50 años después, un equipo de cinco matemáticos finalmente ha demostrado que la meditación de la fiesta del té es cierta. En una preimpresión publicada en enero, establecen un límite en la cantidad de colores que podrían ser necesarios para sombrear los bordes de ciertos hipergráficos para que ningún borde superpuesto tenga el mismo color. Demuestran que el número de colores nunca es mayor que el número de vértices en el hipergráfico.
El enfoque implica dejar de lado con cuidado algunos bordes de un gráfico y colorear otros al azar, una combinación de ideas que los investigadores han utilizado en los últimos años para resolver una serie de problemas abiertos de larga data. No estaba disponible para Erdős, Faber y Lovász cuando soñaron el problema. Pero ahora, mirando su resolución, los dos matemáticos supervivientes del trío original pueden disfrutar de las innovaciones matemáticas que provocó su curiosidad.
“Es un trabajo hermoso”, dijo Lovász, de la Universidad Eötvös Loránd. "Me complació mucho ver este progreso".
Mientras Erdős, Faber y Lovász tomaban té y hablaban matemáticas, tenían una nueva estructura gráfica en sus mentes. Los gráficos ordinarios se construyen a partir de puntos, llamados vértices, unidos por líneas, llamados bordes. Cada borde une exactamente dos vértices. Pero los hipergráficos que Erdős, Faber y Lovász consideraron son menos restrictivos: sus bordes pueden acorralar cualquier número de vértices.
Esta noción más amplia de un borde hace que los hipergráficos sean más versátiles que sus primos de cubo y radio. Los gráficos estándar solo pueden expresar relaciones entre pares de cosas, como dos amigos en una red social (donde cada persona está representada por un vértice). Pero para expresar una relación entre más de dos personas, como la pertenencia compartida a un grupo, cada borde debe abarcar a más de dos personas, lo que permiten los hipergráficos.
Sin embargo, esta versatilidad tiene un precio: es más difícil probar las características universales de los hipergráficos que de los gráficos ordinarios.
“Muchos de los milagros [of graph theory] o desaparecen o las cosas se vuelven mucho más difíciles cuando pasas a los hipergráficos ”, dijo Gil Kalai de IDC Herzliya y la Universidad Hebrea de Jerusalén.
Por ejemplo, los problemas de coloración de los bordes se vuelven más difíciles con los hipergráficos. En estos escenarios, el objetivo es colorear todos los bordes de un gráfico (o hipergráfico) para que dos bordes que se encuentran en un vértice no tengan el mismo color. El número mínimo de colores necesarios para hacer esto se conoce como índice cromático del gráfico.
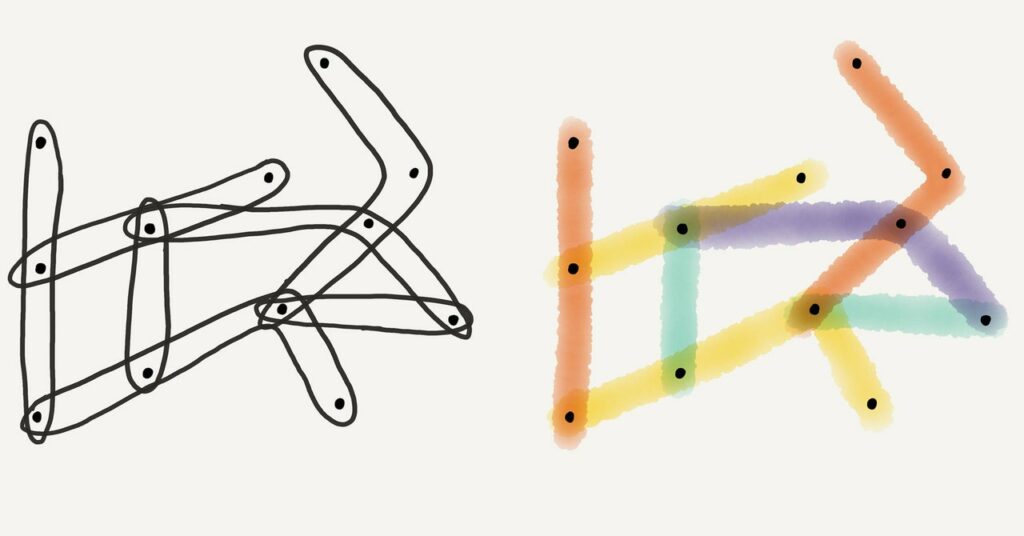
La conjetura de Erdős-Faber-Lovász es una pregunta coloreada sobre un tipo específico de hipergráfico donde los bordes se superponen mínimamente. En estas estructuras, conocidas como hipergráficos lineales, no se permite que dos bordes se superpongan en más de un vértice. La conjetura predice que el índice cromático de un hipergráfico lineal nunca es mayor que su número de vértices. En otras palabras, si un hipergrama lineal tiene nueve vértices, sus bordes se pueden colorear con no más de nueve colores, independientemente de cómo los dibuje.

Otras noticias que te pueden interesar